This tutorial was created for training Python for numerical computation purposes. We are estimating the Hubble Paramter, \(H\) from SDSS data contains redshift \(z\) and velocity \(v\) of 145 galaxies.
Following packages are used in this tutorial.
- Numpy : For numerical computation
- Matplotlib : For visualization
- Scipy : For advanced mathematical operations
1
2
3
4
|
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sc
import scipy.optimize as sp
|
Plotting \(\sin(x)\) and \(\exp(x)\)
1
2
3
4
5
|
x0 = np.linspace(0,10, 100)
y01 = np.sin(x0)
y02 = np.exp(x0)
plt.figure(1,(8,8))
plt.plot(x0,y01,'ro')
|
![png /fitcode/output_4_1.png]()
1
2
|
plt.figure(1,(8,8))
plt.plot(x0,y02,'g')
|
![png /fitcode/output_5_1.png]()
1
2
|
plt.figure(1,(8,8))
plt.plot(x0,y01,x0,y02/20000.)
|
![png /fitcode/output_6_1.png]()
Let us create a set of sata which seems to be linear.
1
2
3
4
5
|
fun0 = np.poly1d([6,3]) #creates a polynomial function 6x+3
print(np.poly1d(fun0))
print(fun0(5)) #evaluates function at x=5
roots=fun0.r #finds the root
print(roots)
|
6 x + 3
33
[-0.5]
1
2
3
4
|
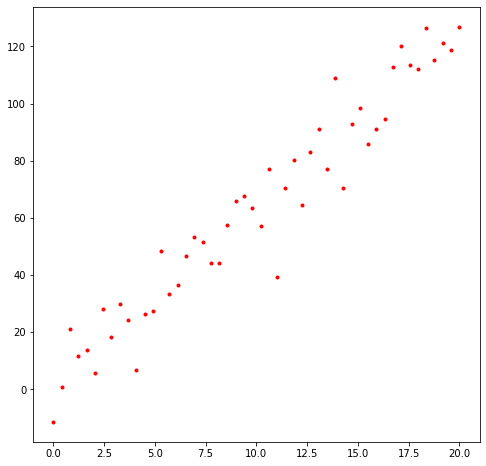
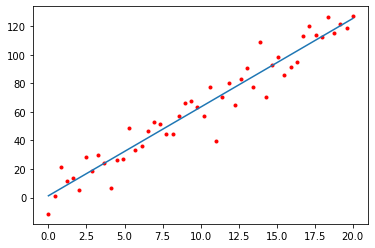
x1 = np.linspace(0,20,50)
y1 = fun0(x1) + 10*np.random.normal(size=len(x1))
plt.figure(1,(8,8))
plt.plot(x1,y1,'r.')
|
![png /fitcode/output_9_1.png]()
1
2
3
|
#method 1 - polyfit from numpy
m1, c1 = np.polyfit(x1,y1,1)
m1,c1
|
(6.20266860427682, 1.2647211366920956)
1
2
3
|
#method 2 - liear regression from scipy
m2,c2, r,p,er = sc.linregress(x1,y1)
m2,c2
|
(6.202668604276818, 1.2647211366921383)
1
2
3
4
|
plt.plot(x1,y1,'r.')
x1_new = np.linspace(0,20,200)
y1_new = np.polyval([m1,c1],x1_new) #polyval creates new function using the fitting parameters we got
plt.plot(x1_new,y1_new)
|
![png /fitcode/output_13_1.png]()
Using poly1d function, a polynomial function \(5x^2-x+3\) is created
1
2
|
fun1 = np.poly1d([5,-1,3]) #creates a polynomial function of 5x^2-x+3
print(np.poly1d(fun1))
|
2
5 x - 1 x + 3
1
2
3
|
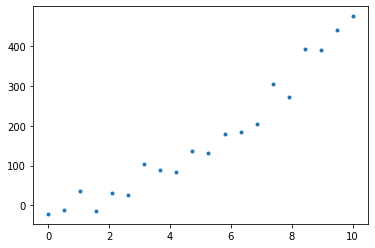
x2 = np.linspace(0,10,20)
y2 = fun1(x2)+25*np.random.normal(size=len(x2))
plt.plot(x2,y2,'.')
|
![png /fitcode/output_16_1.png]()
1
2
3
4
5
6
|
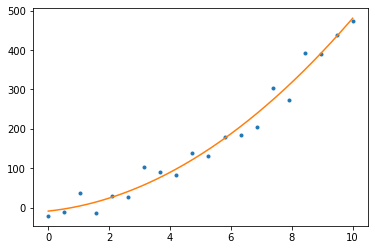
m21,m22, m23 = np.polyfit(x2,y2,2)
x2_new = np.linspace(0,10,200)
y2_new = np.polyval([m21,m22,m23],x2_new)
plt.plot(x2,y2,'.')
plt.plot(x2_new,y2_new)
m21, m22, m23
|
(4.0619455765080215, 8.364517905796896, -9.095626820313775)
![png /fitcode/output_17_1.png]()
1
2
3
4
5
|
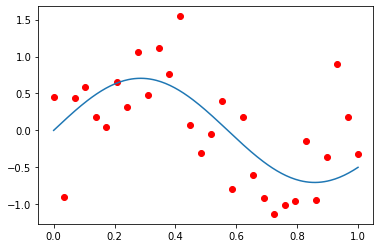
def fun2(x3,a,b):
return a*np.sin(b*np.pi*x3)
p0 = [0.5,2]
x3 = np.linspace(0,1,30)
y3 = fun2(x3,*p0) + 0.5*np.random.normal(size=len(x3))
|
1
2
|
x3_new = np.linspace(0,1,200)
opt,conv = sp.curve_fit(fun2,x3,y3,[-10,4])
|
array([-0.38281612, 3.49268335])
1
2
|
plt.plot(x3,y3,'or')
plt.plot(x3_new, fun2(x3_new,*popt))
|
![png /fitcode/output_21_1.png]()
The above one isn’t probably a best fit. It can be corrected by using appropriate initial values.
Fit and find Hubble parameter
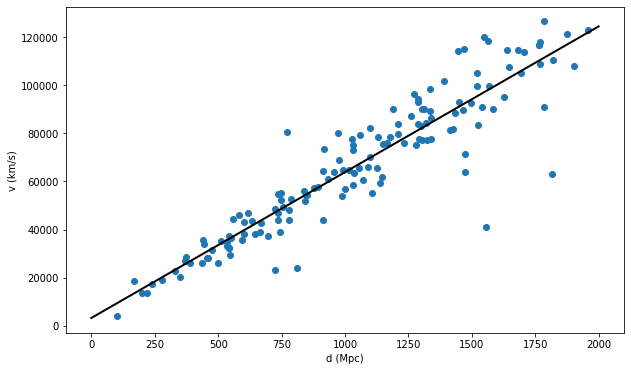
A text file with data, distance(d) and velocities of galaxies (v) can be downloaded from here.
We have to unpack it to read as separate columns and store in z_val and v_val. Now we plot it and fit using Linear regression method. According to Hubble’s Law,
$$v= Hd$$
Thus slope of v versus d plot should give Hubble parameter.
1
2
|
d, v = np.loadtxt("data_sdss.txt",unpack=True) #Import data file "data_sdss.txt"
#and save the columns in two variables
|
1
2
3
4
5
6
7
8
9
10
|
plt.figure(1,(10,6))
plt.xlabel('d (Mpc)') #X label
plt.ylabel('v (km/s)') #Y label
plt.scatter(d,v)
slope, intercept, r_value, p_value, std_err = sc.linregress(d,v)
plt.plot([0, 2000], [intercept, slope * 2000 + intercept], '-k', lw=2)
# here we plot x axis from 0 to 2000, y axis as intercept + slope * x value,
# which gives mx+c, equation of line.
print("Actual value of Hubble Parameter = 69.8")
print('Obtained Value of Hubble Parameter = %1.2f'%slope)
|
Actual value of Hubble Parameter = 69.8
Obtained Value of Hubble Parameter = 60.63
![png /fitcode/output_25_1.png]()
Thus we got the slope, Hubble parameter which is near to the currently estimated value
Least Square Fit Tutorial by Modesto Mas
SDSS modified text file with distance and velocity of galaxies data
Download the whole code as python file